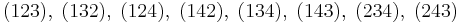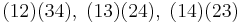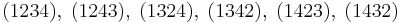Cycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles.[1] This is also called circular notation and the permutation called a cyclic or circular permutation.[2]
Contents |
Definition
be distinct elements of  . The expression
. The expression
denotes the cycle σ whose action is
For each index i,
where 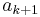 is taken to mean
is taken to mean 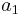 .
.
There are  different expressions for the same cycle; the following all represent the same cycle:
different expressions for the same cycle; the following all represent the same cycle:
A 1-element cycle such as (3) is the identity permutation.[3] The identity permutation can also be written as an empty cycle, "()".[4]
Permutation as product of cycles
Let  be a permutation of
be a permutation of  , and let
, and let
be the orbits of  with more than 1 element. Consider an element
with more than 1 element. Consider an element 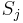 ,
, 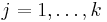 , let
, let 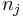 denote the cardinality of
denote the cardinality of 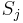 ,
,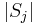 =
=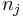 . Also, choose an
. Also, choose an 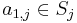 , and define
, and define
We can now express  as a product of disjoint cycles, namely
as a product of disjoint cycles, namely
Note that the usual convention in cycle notation is to multiply from left to right (in contrast with composition of functions, which is normally done from right to left). For example, the product 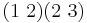 is equal to
is equal to 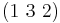 not
not 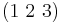 .
.
Example
Here are the 24 elements of the symmetric group on 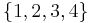 expressed using the cycle notation, and grouped according to their conjugacy classes:
expressed using the cycle notation, and grouped according to their conjugacy classes:
See also
Notes
References
- Dehn, Edgar (1960) [1930], Algebraic Equations, Dover.
- Fraleigh, John (2003), A first course in abstract algebra (7th ed.), Addison Wesley, p. 88–90, ISBN 978-0201763904.
- Hungerford, Thomas W. (1997), Abstract Algebra: An Introduction, Brooks/Cole, ISBN 978-0030105593.
- Johnson, James L. (2003), Probability and Statistics for Computer Science, Wiley Interscience, ISBN 978-0471326724.
This article incorporates material from cycle notation on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
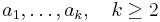

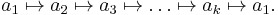

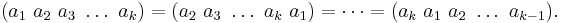
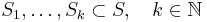
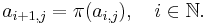
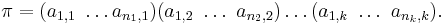
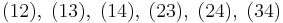 (
(